[7 / 1 / ?]
Hi /sci/,
I know that homework-questions aren't welcome here, but I think this one could be interesting for more people.
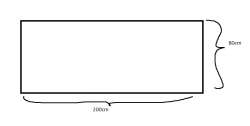
The problem is as follows: You shall prove that when inserting 50 needles in a wall (200cm x 80cm) you will have atleast 2 needles that are at most 30cm apart from each other.
The exercise is for Discrete Maths and we are supposed to use the pidgeon hole principle. My idea was to divide the wall into smaller circles with radiant of 30cm/rectangles with an area of 30cm^2 and show that you can only fit less than 50 circles in it, but I am having proving it
I know that homework-questions aren't welcome here, but I think this one could be interesting for more people.
The problem is as follows: You shall prove that when inserting 50 needles in a wall (200cm x 80cm) you will have atleast 2 needles that are at most 30cm apart from each other.
The exercise is for Discrete Maths and we are supposed to use the pidgeon hole principle. My idea was to divide the wall into smaller circles with radiant of 30cm/rectangles with an area of 30cm^2 and show that you can only fit less than 50 circles in it, but I am having proving it