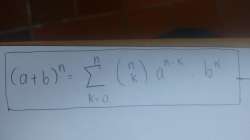/sci/ - Science & Math » Thread #7623702

[15 / 2 / ?]

1MiB, 3264x1836, IMG_20151029_090143598.jpg

Proof

Anonymous Thu 29 Oct 2015 10:03:19 No.7623702 View Reply Report Delete

Quoted By: >>7624390 >>7624401 >>7624458 >>7624782

Okay /sci/ i took your advise and signed up for a class that is all about proofs to really understand math.
Everything was great till this happened
>pic related
Can someone tell how to prove this by matematical induction?

Anonymous

Anonymous Thu 29 Oct 2015 10:11:06 No.7623714 Report Delete

Quoted By:

Gotta show what (a+b)^n+1 is. I'd start by multiplying (a+b)(a+b)^n using the sum formula which is already known to you and see where it gets you

Anonymous

Anonymous Thu 29 Oct 2015 17:15:03 No.7624390 Report Delete

Quoted By: >>7624398

>>7623702
bump to make sure I have time to explain

Anonymous

Anonymous Thu 29 Oct 2015 17:19:37 No.7624398 Report Delete

Quoted By:

>>7624390
Bump so you have time to explain

Anonymous

Anonymous Thu 29 Oct 2015 17:20:30 No.7624401 Report Delete

Quoted By: >>7624417

>>7623702
Proofs by induction involve some sort of indexed sequence - here, (a+b)^n for n=1,2,3,... and so on. When you do a proof by induction there are ALWAYS two steps:

1. Show that the statement is true for the lowest index. Here, show that the statement is indeed true for (a+b)^1.

2. Show that if the statement is true for ANY index N, the statement must then be true for the NEXT index N+1.

Make sure you understand why this works. You've shown that it's true for 1 and if it's true for any index, it's true for the next. Therefore, since it is true for 1, it is true for 2, so it is true for 3, so it is true for 4, on and on to infinity.

The hard part is obviously figuring out how to show that the statement being true for some arbitrary N means it is true for N+1. This is usually where the big idea in an induction proof is found.

Next post: how to figure out the main idea of this proof.

Anonymous

Anonymous Thu 29 Oct 2015 17:26:44 No.7624417 Report Delete

Quoted By: >>7624431

>>7624401
So given that this sum is correct for (a+b)^N, we want to know how to show that it MUST be correct for (a+b)^(N+1) = (a+b) (a+b)^N. We need to figure out the idea behind why this is correct and then demonstrate it in the proof.

Look at a simple case: (a+b)^3 = (a+b) (a+b)^2. Assuming the statement is true for N=2 gives

(a+b) (a^2 + 2ab + b^2) = (a^3 + 2a^2b + ab^2) + (a^2b + 2ab^2 + b^3)

Notice that multiplying the statement by (a+b) gives TWO series, each of which are "offset" in their powers of a^n*b^m. But this is equivalent to an offset in the k index of the original statement. So to combine these to form one sum we should shift the k index of the "b terms". That's the idea here - that's how we're going to recombine these two series to find one series for (a+b)^(N+1).

Anonymous

Anonymous Thu 29 Oct 2015 17:36:54 No.7624431 Report Delete

Quoted By: >>7624440

>>7624417
Applying this to (a+b)^(N+1), we first assume that the statement is true for (a+b)^N. Since (a+b)^(N+1) = (a+b) (a+b)^N, we substitute the summation over k for (a+b)^N and then multiply by (a+b) to get two different sums - one of which is a (a+b)^N and the other is b (a+b)^N.

Now we apply the main idea - shift the index k in the b (a+b)^N sum so that it "matches up" with the a (a+b)^N sum. In that "b sum", let k -> k-1. It becomes a sum from k = 1 to N+1 rather than a sum from k = 0 to N.

Now you just have to recombine these two series by adding them - they should now have the same a^(N+1)+k b^k terms, and you just need to combine the expressions. You'll get one extra term for the N+1 in the series, so then you rewrite it as the sum from k=0 to N+1. If you do it right, you'll see that it's exactly the original statement for N+1.

Anonymous

Anonymous Thu 29 Oct 2015 17:41:00 No.7624440 Report Delete

Quoted By: >>7624859

>>7624431
If any part of that didn't make sense feel free to ask questions.

Anonymous

Anonymous Thu 29 Oct 2015 17:50:43 No.7624458 Report Delete

Quoted By:

>>7623702
draw pascal's triangle, then, show how the n choose k times a^(n-k) times b^k is equal to the sum of the element of pascal's triangle to the upper left and the element of pascal's triangle to the upper right. Next, use this fact to prove that summation from k=1 to (n+1)-1 of n choose k times a^((n+1)-k) times b^k plus a^(n+1) plus b^(n+1) is equal to (a+b) times summation from k=0 to n of n choose k times a^(n-k) times b^k (which, according to your inductive assumption, is just (a+b) times (a+b)^n). Lastly, prove the n = 1 case.

Anonymous

Anonymous Thu 29 Oct 2015 17:52:13 No.7624462 Report Delete

Quoted By:

Also, if you want more sources to help with proofs check out

https://www.reddit.com/r/bibliographies/comments/382937/math_methods_of_proof/

Anonymous

Anonymous Thu 29 Oct 2015 18:32:33 No.7624547 Report Delete

Quoted By:

When you take, for example, (a+b)^3 you get a shitload of terms that have different Permutations of a&b :

aaa = a^3

baa = a^2b
aba = a^2b
aab = a^2b

bba = b^2a
abb = b^2a
bab = b^2a

bbb = b^3

When you add the same terms together... :

a^3+3a^2b+3ab^2+b^2

...you are literally throwing away the importance of order which is ofcours the Combinations of a&b.

And there you have it.

Anonymous

Anonymous Thu 29 Oct 2015 19:22:35 No.7624665 Report Delete

Quoted By:

just look it up in a book

Anonymous

Anonymous Thu 29 Oct 2015 19:24:39 No.7624669 Report Delete

Quoted By:

use method of undetermined coefficients

Anonymous

Anonymous Thu 29 Oct 2015 20:00:55 No.7624782 Report Delete

Quoted By:

>>7623702
>>7623702

It should go something like this, I started it but I'm to lazy and it's too much work to finish it. Your next step should be express the sum as additions and distribute the (a+b)
Let
$P(n):(a+b)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}b^{k}$

To prove by induction that $P(n)$ is valid $\forall n$ we must prove:
1. $P(1)$
2. $P(q) \rightarrow P(q+1)$

Proceed:
1. I'll let you do this proof, it's nothing hard

2. Prove $P(q) \rightarrow P(q+1)$
Where:
$P(q):(a+b)^{q}=\sum_{k=0}^{q}\binom{q}{k}a^{q-k}b^{k}$
$P(q+1):(a+b)^{q+1}=\sum_{k=0}^{q+1}\binom{q+1}{k}a^{q-k}b^{k}$

So we start:
$(a+b)^{q+1}=(a+b)^{q}(a+b)=(\sum_{k=0}^{q}\binom{q}{k}a^{q-k}b^{k})(a+b)$ (because of hypothesis)
Then:
$\sum_{k=0}^{q}\binom{q}{k}a^{q-k}b^{k}= \binom{q}{0}a^{q-0}b^{0}$

Anonymous

View Same Google ImgOps iqdb SauceNAO binomial_coefficients.png, 88KiB, 686x894

Anonymous Thu 29 Oct 2015 20:25:56 No.7624859 Report Delete

Quoted By:

>>7624440
Didn't hear a reply, so here's the proof. You can check it against your work.

Subject

Name

E-mail

Password

Capcode	All Only User Posts Only Verified Posts Only Moderator Posts Only Manager Posts Only Admin Posts Only Developer Posts Only Founder Posts
Show Posts	All Only With Images Only Without Images Only Spoiler Images Only Non-Spoiler Images
Deleted Posts	All Only Deleted Posts Only Non-Deleted Posts
Ghost Posts	All Only Ghost Posts Only Non-Ghost Posts
Post Type	All Only Sticky Threads Only Opening Posts Only Reply Posts
Results	All Grouped By Threads
Order	Latest Posts First Oldest Posts First

On these boards

Your latest searches

Proof